Download
paper   DOI image/svg+xml DOI DOI doi   arXiv image/svg+xml arXiv arXiv arXiv  
Abstract

For a finite graph, we establish natural isomorphisms between eigenspaces of a Laplace operator acting on functions on the edges and eigenspaces of a transfer operator acting on functions on one-sided infinite non-backtracking paths. Interpreting the transfer operator as a classical dynamical system and the Laplace operator as its quantization, this result can be viewed as a quantum-classical correspondence. In contrast to previously established quantum-classical correspondences for the vertex Laplacian which exclude certain exceptional spectral parameters, our correspondence is valid for all parameters. This allows us to relate certain spectral quantities to topological properties of the graph such as the cyclomatic number and the 2-colorability. The quantum-classical correspondence for the edge Laplacian is induced by an edge Poisson transform on the universal covering of the graph which is a tree of bounded degree. In the special case of regular trees, we relate both the vertex and the edge Poisson transform to the representation theory of the automorphism group of the tree and study associated operator valued Hecke algebras.

Citation
@article {AFH25,
  AUTHOR = {Arends, Christian and Frahm, Jan and Hilgert, Joachim},
  TITLE = {Edge {L}aplacians and edge {P}oisson transforms for graphs},
  JOURNAL = {Potential Anal.},
  FJOURNAL = {Potential Analysis},
  VOLUME = {63},
  YEAR = {2025},
  PAGES = {631--677},
  URL = {https://doi.org/10.1007/s11118-024-10184-y},
}

Theorem C suggests that the dimension of certain energy-preserving functions on the edges of a directed graph is connected to the topology of the underlying undirected graph. Specifically, a function is considered energy-preserving if it assigns a weight to each directed edge such that, at every vertex, the sum of incoming weights equals the sum of outgoing weights. The number of linearly independent energy-preserving functions matches the number of independent cycles of the underlying undirected graph, known as the cyclomatic number. Below is an example with six independent cycles and the associated independent energy-preserving functions.

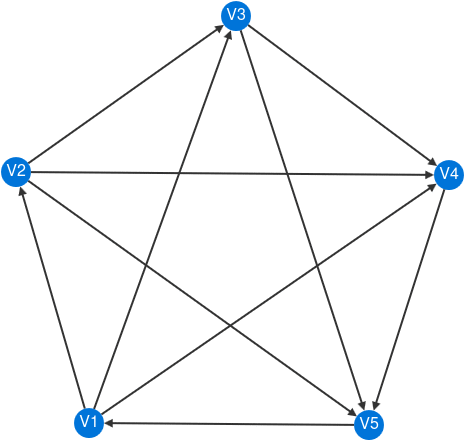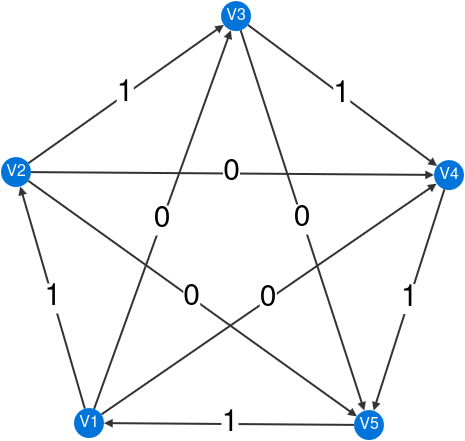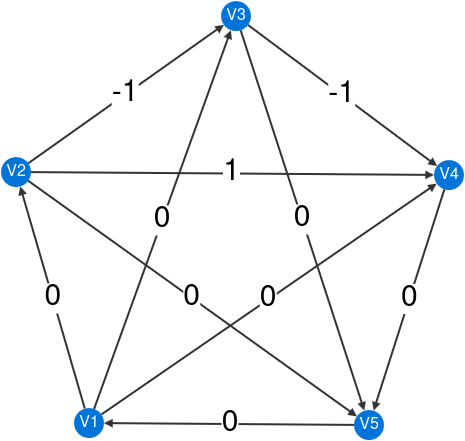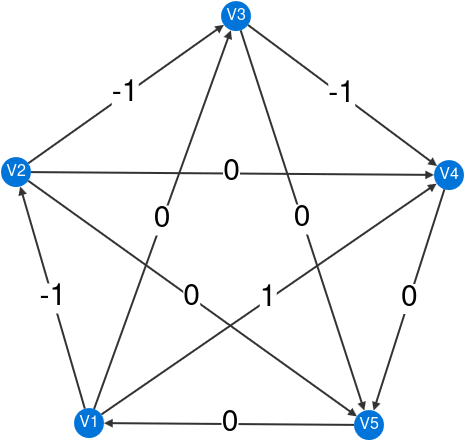
Example graph

Explore your own graph interactively here.